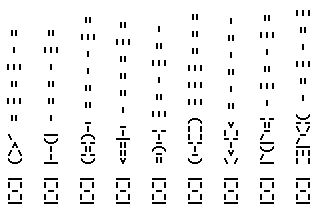Merkles Puzzle

Übersicht

-- Merkles Puzzle ist ein von Ralph Merkle 1974 erfundenes Verfahren, um trotz abgehörter
    Verbindung einen geheimen Code-Schlüssel zwischen Sender und Empfänger zu vereinbaren.

-- Es ist von überragender Bedeutung,  weil es als erstes solches Verfahren der Beweis war, dass so
    etwas überhaupt möglich ist.   Es hat auch deshalb einen hohen Bildungswert, weil es sehr einfach
    und leicht verständlich ist und keine Mathematik benötigt.

Ich schreibe diesen Artikel, weil ich keine didaktisch gute Beschreibung im Internet fand.
Zuerst definieren wir kurz, was ein Verschlüsselungsverfahren und was ein Schlüssel ist.

Was ist ein Verschlüsselungsverfahren?

Ein Verschlüsselungsverfahren ist ein Verfahren, um Daten (z.B. einen Text) in eine unverständliche Form zu bringen, die - bei entsprechender Kenntnis - wieder in den Originaltext zurückverwandelt werden kann.

Beispiel: Buchstabenversetzung: Man ersetzt jeden Buchstaben eines Textes durch den Buchstaben, der im ABC 3 Stellen weiter hinten steht. Beispielsweise wird A durch D ersetzt. Das Ganze funktioniert zyklisch, also auf Z folgen A B C ...

Was ist ein Schlüssel?

Im obigen Beispiel ist die Buchstabenversetzung das Verschlüsselungsverfahren. Die Zahl 3 ist der Schlüssel.     2 wäre ein anderer Schlüssel (man nimmt den übernächsten Buchstaben).

Ein mechanisches Beispiel:   Der Mechanismus eines Zahlenschlosses ist quasi das Verschlüsselungsverfahren, die öffnende Ziffernkombination der Schlüssel.

Das Problem: einen geheimen Schlüssel vereinbaren

A will von England aus an B in Australien verschlüsselte Daten über eine unsichere (abgehörte) Leitung senden.

- Man verwendet ein öffentlich bekanntes Verschlüsselungsverfahren.
- Es gab keine Möglichkeit, vorher einen geheimen Schlüssel zu vereinbaren.

Ist es möglich, über eine abgehörte Leitung einen geheimen Schlüssel zu vereinbaren, den nur A und B kennen?

Die Lösung:   Merkles Puzzle

Ja, das ist möglich, und zwar folgendermaßen:

- A sendet an B eine lange Tabelle, die im Klartext z.B. so aussehen könnte:

decodiert?	Zeilenname	langer Schlüssel
Bingo	Banane	0123456789012345
Bingo	Orange	0011223344556677
. . .	. . .	. . .
Bingo	Apfel	0001112223334445
. . .	. . .	. . .
Bingo	Tabak	2345123467894568

- A verschlüsselt aber vor dem Senden jede Zeile der Tabelle mit einem anderen kurzen Schlüssel.

- B pickt sich irgendeine Zeile heraus und versucht, diese zu decodieren.
  Dazu probiert er alle Schlüssel durch.   Der Schlüsselbereich (z.B. alle Zahlen mit 10 Binärstellen)
  wurde von A vorgegeben.   Wenn das Ergebnis mit "Bingo" anfängt, war der Versuch erfolgreich.

- B sendet den Zeilennamen zurück an A

- Mit dem in der Zeile angegebenen langen Schlüssel codieren nun A und B ihre Botschaften

Beispiel: B pickt sich eine Zeile heraus, decodiert sie, sendet den Zeilennamen "Apfel" an A.
                Mit dem langen Schlüssel in dieser Zeile codieren jetzt A und B ihre Nachrichten.

Der Schlüssel zur Entzifferung einer Zeile muss kurz sein, damit B in angemessener Zeit die gewählte Zeile entziffern kann. Aber der Schlüssel für die weitere Kommunikation zwischen A und B muss viel länger sein, damit eine Entschlüsselung für einen Abhörer unmöglich ist.



Sicherheit
Angenommen, A sendet eine verschlüsselte Tabelle mit 10¹⁰ Einträgen. (Das ist nur per Computer-erzeugter Tabelle zu schaffen). Und angenommen, B braucht zur Entschlüsselung der ausgewählten Zeile 1 Sekunde.   Ein Abhörer muss durchschnittlich die Hälfte aller Zeilen entschschlüsseln, bis er die Zeile mit dem Namen findet, den B an A zurückgeschickt hat.   Er braucht also durchschnittlich 10¹⁰/2 Sekunden ~ 158 Jahre


Die größte Gefahr ist, dass ein Abhörer zufällig sofort dieselbe Zeile decodiert, die B ausgewählt hat Die Wahrscheinlichkeit dafür ist allerdings nur 1 zu 10¹⁰/2

Doch man kann diese Gefahr durch folgende Maßnahme ausschalten:
B wählt über die ganze Tabelle verteilt mehrere Zeilen aus (z.B. 10), decodiert sie und sendet die Namen an A. Die langen Schlüssel dieser Zeilen bilden aneinandergereiht den geheimen Schlüssel für die weitere Kommunikation. Ein Abhörer muss jetzt fast die ganze Tabelle entschlüsseln, bis er alle verwendeten Zeilen findet

Jetzt kann man u.U. auf die Angabe eines langen Schlüssels in jeder Zeile verzichten, und tut stattdessen folgendes:   B merkt sich, mit welchen Schlüsseln er jede Zeile entziffert hat, und setzt diese zu einem langen Schlüssel zusammen.   Auch A setzt aus den zurückgesendeten Zeilennamen den Gesamtschlüssel zusammen, er weiß ja, mit welchem kurzen Schlüssel jede Zeile codiert wurde.


Fazit
Merkles Puzzle ist kein Verschlüsselungsverfahren im engeren Sinne, sondern eine Methode zur
Vereinbarung eines geheimen Schlüssels für ein solches Verfahren trotz abgehörter Leitung.
Es benötigt selbst ein Verschlüsselungsverfahren (für die Tabelle).




Eher scherzhaft:   Merkles Puzzle in Lautbildschrift
Eine Lautbildschrift ist eine Bilderschrift und gleichzeitig eine echte Lautschrift. Denn ihre Bildsymbole werden aus den Buchstaben eines speziellen Alphabets linear zusammengesetzt. Die Schreibrichtung ist senkrecht von unten nach oben.   Man schreibt also spaltenweise, nicht zeilenweise.

Man kann als Tabelle für Merkles Puzzle auch einen Lautbildschrift-Text entwerfen.
Er könnte beispielsweise (unverschlüsselt) so aussehen:





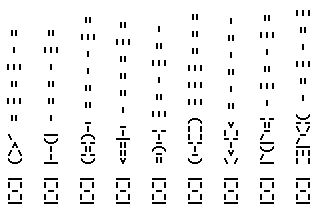
Jede Spalte repräsentiert eine Verschlüsselung:
- Der Sockel ist das Bingo-Signal, dass die Spalte richtig entschlüsselt wurde.
- Das Ding auf dem Sockel ist der Zeilenname.
- Die Zahl darüber (in Strichziffern) ist der lange Schlüssel für die weitere Kommunikation.
Die Spalten müssen mit Leerzeichen gleiche Länge haben, oder ein Trennzeichen.

Das Ganze ist eine in Spalten (nicht wie oben in Zeilen) gegliederte Tabelle - und gleichzeitig ein korrekter Text der Lautbildschrift. Die Szene ähnelt dem Inneren eines Museums. Er sieht aus wie eine Reihe von Sockeln, auf denen Dinge aufgestellt sind (Birne, Stielglas. Geige, Schwert, Mensch, Eierkopf, lustiges Gesicht, Känguru, Kuh).   Zahlen über Dingen geben in Lautbildschrift eigentlich die Anzahl des Dings darunter an.
Man könnte eine solche Tabelle auch entwerfen als Pflanzen in (immer gleichen) Töpfen, oder als Ausstellung von Büsten, oder als Allee mit Standbildern und Pflanzen (alle auf gleichen Sockeln), oder als Zoo (Tiere hinter immer gleichen Gittern), oder als Büfett (Speisen auf immer gleichen Tischen).

Eine solche Tabelle in Lautbildschrift ist interessant und unterhaltsam anzusehen. Das Ganze ist aber eher scherzhaft, denn weil eine solche Tabelle sehr groß sein muss, wird sie per Computer entworfen, und niemand schaut die Tabelle wirklich an (und wenn, dann kennt ja nur der Sender A die ganze Tabelle).
Eine solche Tabelle in Lautbildschrift wäre nur im Telegrafenzeitalter sinnvoll gewesen, als man noch "von Hand" codierte.

Homepage  Leonhard Heinzmann                          Stand:  14. 12. 2022